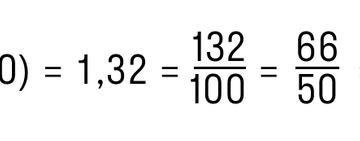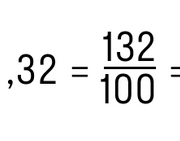1/5 — одна пятая. конвертер величин

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби. 

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

• Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
  8 < 12
  12 > 8
• Это значит, что < Изи!

Пример 2. Сравните дроби:

• Как и в прошлом примере, знаменатели дробей — равны. Сравниваем числители:
  9  > 10
  1 < 10
• Это значит, что >

Пример 3. Сравните дроби:

• Знаменатели дробей снова равны. Сравниваем числители:
  3  > 1
  1 < 3
• Это значит, что >

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель. 

Давайте разберем наглядный пример сравнения дробей:

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
 

• Запишем в виде дробей: и
• А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
  6  > 5
  5 < 6.
• Это значит, что >

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого. 

12 — 7 = 6
12 — уменьшаемое
7 — вычитаемое
5 — разность

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы». 

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
 

Пример 1. Найдите разность:

Вычитаемая дробь меньше уменьшаемой

Выполняем вычитание:

Пример 2.Найдите разность:

• Смешанные дроби превращаем в неправильные:
• Чтобы сравнить дроби с разными числителями и знаменателями, нужно привести их к общему знаменателю:
• Наименьшее общее кратное — 40
  40 : 8 = 5
  40 : 5 = 8
• Умножаем первую дробь на дополнительный множитель 5:
• Умножаем вторую дробь на дополнительный множитель 8:
• Дроби приведены к общему знаменателю:

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

Мы видим, что вычитаемое меньше уменьшаемого, значит можем без труда найти разность:

Основные правила

Как мы определились, правильно выбрать размеры охотничьей дроби – очень важно, если не первостепенно. Так что нужно следовать следующим рекомендациям, которые помогут определить, какой номер на какую дичь использовать

При охоте на рысь или волка стоит запастись картечью с диаметром не меньше 5,25 миллиметров. Для волка можно взять диаметр крупнее, однако не более 10 миллиметров. Поразить рысь можно также и дробью размером 4/0 (d = 5 миллиметров) и № 3/0 (d = 4,75 миллиметров).

На всю остальную дичь нужно охотиться только дробью, при этом помня, что животное умрет от болевого шока, если в него попало 5-6 дробин.

Лисица, тетерев, глухарь, заяц. При охоте на них зимой и осенью будут успешно поражены дробью номер 1 – 4.

При охоте на уток мелкого размера и молодого тетерева, а также молодых крупных уток летом следует брать дробь номер 5 – 7. Такие же правила действуют и для охоты на куропатку, рябчика и вальдшнепа.

При охоте на гуся и взрослого глухаря в осенне-зимний период рекомендуется использовать дробь номер 2/0 и 0.

А вот на бекаса и перепелку рекомендовано ходить с дробью маленького диаметра – калибр для охоты 8 – 10.

Если вы собираетесь охотиться стальной дробью, то ее подобрать будет также нетрудно. Нужно просто взять размер свинцовой дроби и увеличить на 2 пункта. Причем, в номерах это выглядит наоборот в сторону уменьшения (у дроби с наибольшим номером наименьший диаметр). Так, например, если вы идете на бекаса и перепелку со стальными дробинами, то вам понадобится номер 6 – 8. Их диаметр составляет уже соответственно 4,25; 4; 3,75 миллиметров.

Дробь по видам дичи

Предположим, что охотнику удастся выстрелить дробью двенадцатого номера по зайцу и убить его (к примеру, увеличив довеску пороха). От подранка в этом случае останется куча дыр и море крови. Трофейная ценность шкуры полностью пропадет, и из мяса придется выковыривать несколько десятков свинцовых шариков. Поэтому определенные номера дроби рекомендуется использовать только для отстрела конкретных животных:

Вид дичи	Номер дроби
Волки, косули, олени, кабаны, лоси и другие крупные звери, кроме медведей	00, 000 и 0000
Зайцы, лисы, белки и прочие мелкие пушные зверьки и млекопитающие	2, 1 и 0
Тетерева, глухари, утки, гуси и другие птицы крупного размера	6, 5, 4 и 3
Куропатки, чирики, рябчики, вальдшнепы и прочие разновидности птиц среднего размера	8 и 7
Дупели, кулики, бекасы, перепелки и другие мелкие разновидности птиц	11, 10 и 9

Что касается более крупных зверей, то для их отстрела лучше всего использовать картечь. Если же охотник планирует добыть воробья или другую разновидность мелкой птицы дробью, то тут пригодится баллистический снаряд под номером 12.

Свинцовая дробь №10 на мелкую пернатую дичь

Зависимость от времени года

Размер добычи может меняться в течение всего года. Большинство птиц и млекопитающих ближе к зиме начинают наращивать оперение и пух, через который дробинам сложно пробиться. Так что баллистический снаряд, который использовался весной, может оказаться не столь эффективным при охоте в конце осени. Именно поэтому при выборе дроби следует учитывать время года:

1. Зимой рекомендуемый показатель номера дроби можно увеличить на одну единицу. То есть если для отстрела лисы обычно использовался шарик нулевого номера, то его следует заменить на первый, поскольку звери во время холодов теряют большую часть веса.
2. Весной большинство животных достигают минимального показателя массы за все время года, так что номер дроби следует выбирать на 1-2 меньше, нежели осенью или летом. Особенно это касается пернатой дичи, которая возвращается из теплых краев.
3. Летом охотник может смело использовать те номера дроби, которые перечислены в таблицах в предыдущем разделе, поскольку масса животного в течение всех трех месяцев остается в пределах нормы.
4. Осенью многие птицы и млекопитающие набирают в весе, так что для их отстрела придется обзавестись более крупной дробью, то есть уменьшить номерной показатель на пару единиц, например, переключиться с тройки на единичку.

Выбор дроби в зависимости от времени года

Эти рекомендации являются условными, поскольку многое зависит от конкретного зверя и того, в каком именно месяце он начинает набирать жир. В большинстве случаев данные советы работают, так что начинающие охотники могут смело ими пользоваться.

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8
• 7,42
• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Как решаем:

Ответ:.

• По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
• Наименьшее общее кратное — 15:
  15 : 15 = 1
  15 : 5 = 3
• Умножаем первую дробь на дополнительный множитель 1:
• Умножаем вторую дробь на дополнительный множитель 3:
• Дроби приведены к общему знаменателю:
• Сравниваем числители получившихся дробей: 3 < 6

Пример 4. Найдите разность:

Как решаем:

• Смешанные дроби превращаем в неправильные:
• Чтобы сравнить дроби с разными числителями и знаменателями, нужно привести их к общему знаменателю.
• Наименьшее общее кратное — 42:
  42 : 7 = 6
  42 : 6 = 7
• Умножаем первую дробь на дополнительный множитель 6:
• Умножаем вторую дробь на дополнительный множитель 7:
• Дроби приведены к общему знаменателю.
• Если знаменатели одинаковые — больше та дробь, числитель которой больше.
  Мы видим, что вычитаемое меньше уменьшаемого, значит можем найти разность:

Ответ:

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
      
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
       
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.

Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.

В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

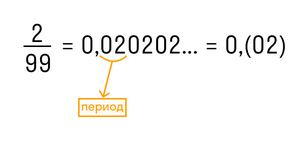
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Виды периодических дробей: чистые и смешанные.

Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).

Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.

Рассмотрим примеры дробей, чтобы научиться определять части и период.

1/3 = 0,3333… = 0,(3)

Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Читаем так: ноль целых три в периоде.

7/12 = 0,583333… = 0,58(3)

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.

17/11 = 1,545454… = 1,(54)

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Читаем так: одна целая пятьдесят четыре сотых в периоде.

25/39 = 0,641025 641025… = 0,(641025)

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.

Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.

пятьдесят четыре сотых в периоде.

9200/3 = 3066,666… = 3066,(6)

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями. 

Запомните правило:

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  9  > 7
  7 < 9
• Значит, дробь с меньшим знаменателем — больше:

Пример 2. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  10  < 11
  11 > 10
• Значит дробь с меньшим знаменателем — больше:

Пример 3. Сравните дроби:

• У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
  6  > 3
  3 < 6
• Значит, дробь с меньшим знаменателем — больше.

Для наглядности представим ситуацию, в которой вам предстоит разделить торт между тремя друзьями. Это значит, что 6 кусков торта равномерно распределяются по 3 людям: каждому достается 6:3 = 2 по 2 кусочка. 

А теперь представим более приятную ситуацию: кусков торта по-прежнему 6, а друзей уже только 2. Тогда каждому достанется по 3 вкуснейших кусочка:

Как видите, сравнение дробей может вам пригодиться в самых неожиданных ситуациях. Теперь, когда снова придется хорошенько задуматься о соотношении кусков торта и приглашенных гостях, изученная тема поможет вам принять верное решение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

Как решаем:

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
      
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
                  
• делить и умножать уравнение на 0 нельзя.
              

Универсальный алгоритм решения

1. Определить область допустимых значений.

                   

2. Найти общий знаменатель.

                   

3. Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

                   

4. Раскрыть скобки, если нужно и привести подобные слагаемые.

                   

5. Решить полученное уравнение.

                   

6. Сравнить полученные корни с областью допустимых значений.

                   

7. Записать ответ, который прошел проверку.

               

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
      
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа.              Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а;                  если а равно нулю, а b не равно нулю — у уравнения нет корней;                  если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.
2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ: 16/10 = 1,6.

Пример 2. Перевести 37/1000 в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Так как в числителе только две цифры, то на пустующие места пишем нули.
4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ: 37/1000 = 0,037.

Время года имеет значение

В наших рекомендациях период охоты указан совсем не случайно. Все дело в том, что в зависимости от времени года разниться и то, какой калибр для охоты используется. Причем, чем холоднее, тем больше будет диаметр дроби. Разница будет составлять те же 2 номера между летом – началом осени и поздней осенью – зимой. Это объясняется вовсе не температурой воздуха, поскольку на выстрел она никак не влияет, а различными особенностями самих животные, которые «утепляются» к холодам, поэтому, чтобы наверняка удалось пробиться через густое оперение, подшерсток или шерсть нужно увеличить калибр снарядов.

Таблица — «Какие патроны на какую дичь»

Объект охоты	Апрель-Май	Август-Сентябрь	Октябрь-Ноябрь	Декабрь-Январь
Бекас, кулики, перепел, дупель	—	8-10	7-10	—
Чирки	5-6	6-7	5-6	—
Вальдшнеп	7-8	8-9	6-7	—
Рябчик	—	6-7	5-6	3-5
Тетерев-косач	3-5	5-6	3-5	2-3
Нырок, кряковая утка	4-5	5-6	3-4	—
Глухарь	2-0	1-0	0-00	0-00
Заяц	—	—	2-3	2-0
Гусь	1-00	—	0-00	—
Лиса	—	—	2-0	1-0
Волк	—	—	6/0	5/0-6/0
Рысь, косуля	—	—	000-0000

Перевод периодической дроби в обыкновенную

Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.

Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.

Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:

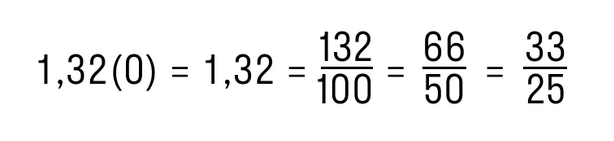
Вот и ответ!

Рассмотрим пример, в котором период дроби отличен от нуля.

Как записать периодическую дробь 10,0219(37) в виде обыкновенной:

1. Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k.

   В нашем примере k = 2.

2. Считаем количество цифр, которые стоят после запятой, но до периода десятичной дроби. Обозначаем количество цифр буквой m.

   m = 4.

3. Запишем все цифры после запятой: в том числе и цифры из периода в виде натурального числа.

   Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.

   a = 021937 = 21 937

4. Теперь запишем все цифры, которые стоят после запятой, но до периода, в виде натурального числа. Если вначале до первой значащей цифры идут нули, то отбрасываем их. Обозначим полученное число — b.

   b = 0219 = 219

5. Подставляем найденные значения в формулу, где Y — целая часть бесконечной периодической дроби.

   Y = 10

Теперь осталось подставить все найденные значения в формулу и получить ответ:

Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.

Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:

0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + ..

Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q).

Пример. Перевести периодическую дробь 0,(7) в обыкновенную.

Как решаем:

1. Запишем 0,(7) = 0,7 + 0,07 + 0,007 + ..

   Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1.

2. Применим формулу b/(1-q):

   0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 — 0,1) = 0,7/0,9 = 7/9.

Ответ: 7/9.

Итак, есть два вида периодических дробей. Сейчас расскажем, чем отличаются способы их преобразования в обыкновенные дроби.

Виды дроби

Дробь используется для охоты на самых различных животных: глухарь, волк, заяц, тетерев, утка, белка, кабан. Так что было бы странно, если бы один и тот же баллистический снаряд подходил для отстрела как хищника, так и мелкого пушного зверя. Поэтому разновидностей дроби существует немало, а для удобства выбора баллистический снаряд классифицируют по типу материала, а также диаметру шарика.

Материал

Основные разновидности дроби изготавливают из металла, отличающегося разной массой и показателем деформации. Некоторые боеприпасы могут быть использованы только при стрельбе из определенного оружия, к примеру, каленая дробь разорвет любой ствол, который выполнен из углеродистой стали. Вот основные разновидности, пользующиеся популярностью у охотников:

1. Свинцовая дробь. Самый распространенный и дешевый вид баллистического снаряда. Ввиду того, что при производстве используется достаточно легкий и мягкий металл, такая дробь подойдет для отстрела только небольших животных и птиц.
2. Стальная дробь. Для изготовления этого поражающего элемента используется углеродистая сталь, отличающаяся хорошей прочностью и высокой массой. Мощность выстрела у такого патрона убойная, вот только дробинки могут наносить повреждения каналам ствола.
3. Каленая дробь. Отличается от свинцовой разновидности лишь тем, что шарики проходят процедуру холодной закалки. Такой баллистический снаряд подойдет только для прочных стволов, а скорости выстрела вполне хватит, чтобы завалить медведя гризли.

Дробь свинцовая охотничья омедненная №1

Еще есть плакированная дробь — самый дорогой, но самый лучший (по характеристикам) вид баллистического снаряда. Такие шарики изготавливаются из свинца, но покрываются слоем никеля, из-за чего весят они достаточно мало, однако обладают внушительной поражающей силой.

Диаметр дроби по номерам

Чем больше диаметр баллистического снаряда, тем меньше свинцовых боеприпасов вместится в патрон, но тем выше будет кучность стрельбы и мощность выстрела. Крупная дробь используется в основном для отстрела млекопитающих внушительной массы, маленькая — подойдет для охоты на птиц. В таблице перечислен размер по номерам (показатели актуальны для тех патронов, которые изготавливаются в России):

Номер дроби	Диаметр дроби (мм)
12	1,25
11	1,50
10	1,75
9	2,00
8	2,25
7	2,40
6	2,75
5	3,00
4	3,25
3	3,50
2	3,75
1	4,00
4,25
00	4,50
000	4,75
0000	5,00

Маркировка патронов в остальном мире немного отличается о российской продукции, но основные показатели сохраняются. Вот номера дробинок и их диаметр:

Номер дроби	Диаметр дроби (мм)
12	1,25
11	1,50
10	1,75
9	2,00
8	2,25
7	2,40
6	2,75
5	3,00
4	3,25
3	3,50
2	3,75
1	4,00
4,25
BB	4,50
BBB	4,75
T или O	5,00

Таким образом, чем меньше номер дроби, тем для более крупного зверя она используется. К примеру, №0000 подойдет для отстрела молодых оленей и лосей, а поражающей силы №12 едва ли хватит для того, чтобы сбить перепелку. Хотя размер добычи — далеко не единственный показатель, который следует учитывать.

Виды дроби

Согласно ГОСТу, дробь изготавливают либо методом штамповки, либо литьем. Бывает она мягкой и твердой. Мягкая бывает только охотничьей, она маркируется литерами ОМ. Вторая, соответственно, подразделяется на охотничью (ОТ) и спортивную (СТ). Помимо этих букв, при обозначении описываемых снарядов могут использоваться и другие литеры. Например, буква Ш означает, что дробь изготовлена штамповкой, а буква Л – что методом литья.

Кроме буквенного обозначения, у каждой дроби есть еще и цифровое, номера дроби дают представление о ее диаметре. У самой крупной дроби диаметр 5 миллиметров и обозначается четырьмя нулями. У самой маленькой номер 12. Диаметр такой дроби составляет всего 1,25 миллиметра. Причем, каждая следующая цифра означает изменение диаметра на 0,25 мм. Таким образом, номер 11 будет иметь размер 1,5 миллиметра; № 9 – 2 миллиметра и т.д.

Есть еще одна особенность. Иногда дробь охотничья крупного диаметра обозначается нулями, иногда указывается их количество. Например: дробь диаметром 5 миллиметров, как отмечалось ранее, имеет номер 0000 или 4/0.

Дроби для охоты диаметром 4,75 миллиметров – это номер 000 или 3/0.

У дроби диаметром 4,5 мм — номер 00 или 2/0.

Диаметр 4,25 миллиметров – это номер 0 или 1/0.

Далее следует обычная нумерация, которая свидетельствует об уменьшении размера диаметра на 0,25 миллиметров. Так, у номера 0 будет диаметр 4 миллиметров, у номера 1 – 3,75 миллиметров и т.д.

Также необходимо помнить о том, что 1, 2 дробины не поразят дичь, даже при попадании прямо в сердце. Например, утка с таким ранением может улететь на добрый километр, гусь – даже дальше. Заяц тоже не сразу падает замертво, еще какое-то время он несется во весь опор. Причем хорошо, если это происходит на открытой местности, так как если он уйдет в осоку или бурьян, то найти его будет очень непросто.

В этом смысле самым выносливым является фазан, даже с ранением сердца он способен пробежать десяток километров.

И это мелочи, если сравнивать с тем, что может произойти, если ранить крупную дичь. Например, кабана. Озверев, он вполне способен побежать прямо к охотнику, а не от него. И тут последствия могут быть довольно плачевными.

Так что одного меткого выстрела недостаточно. Он должен быть сразу смертельным

Поэтому крайне важно выбрать правильный калибр для охоты

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.