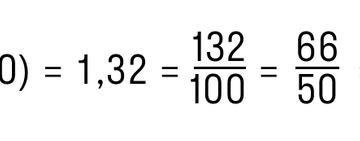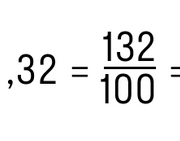Как перевести периодическую дробь

Натуральное число как дробь со знаменателем 1

Знаменатель обыкновенной дроби может быть равен единице. В таком случае возможно говорить, что рассматриваемый предмет (величина) неделим, являет собой нечто целое. Числитель в подобной дроби укажет, какое количество таких предметов взято, т.е. обыкновенная дробь вида m1 имеет смысл натурального числа m. Это утверждение служит обоснованием равенства m1 = m.

Запишем последнее равенство так: m = m1.  Оно даст нам возможность любое натуральное число использовать в виде обыкновенной дроби. К примеру, число 74 – это обыкновенная дробь вида 741.

Определение 5

Любое натуральное число m возможно записать в виде обыкновенной дроби, где знаменатель – единица: m1.

В свою очередь, любая обыкновенная дробь вида m1 может быть представлена натуральным числом m.

Перемена знаков у членов дроби

Если числитель и знаменатель дроби заменить величинами, им противоположными, то значение дроби не изменится, так как эта операция равносильна умножению числителя и знаменателя на одно и то же число —1. Например,

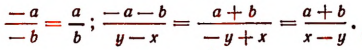
Если числитель дроби заменить величиной, ему противоположной, и при этом переменить знак, стоящий перед дробью, на противоположный, то получится выражение, равное первоначальному.

Например:

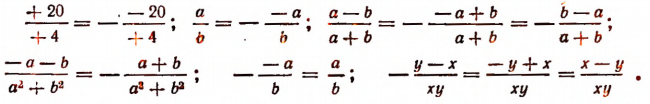
Если знаменатель дроби заменить величиной, ему противоположной, и при этом переменить знак, стоящий перед дробью, на противоположный, то получится выражение, равное первоначальному.

Например:

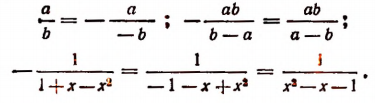
Примечание. Так как а — b и b — а являются величинами противоположными, то всегда представляет собой минус единицу, если только

Если же а = b , то выражение обращается в и потому смысла не имеет.

Вариант 3: Дробь с горизонтальным разделителем

Добавить в текстовый документ Ворд дробь с горизонтальным разделителем между числителем и знаменателем можно одним из двух методов – используя средства вставки уравнений или специальный код с его последующим преобразованием.

Способ 1: Вставка формулы

В Microsoft Word имеется набор инструментов для работы с математическими выражениями, для чего можно как использовать уже готовые формулы и уравнения (например, бином Ньютона или площадь круга), так и «собирать» их самостоятельно из более простых записей. В числе последних есть и интересующая нас в рамках настоящей статьи дробь с горизонтальным разделителем.

1. Откройте вкладку “Вставка” и выберите в группе “Символы” пункт “Уравнение”.

1. Нажав на кнопку “Уравнение”, выберите пункт “Вставить новое уравнение”.

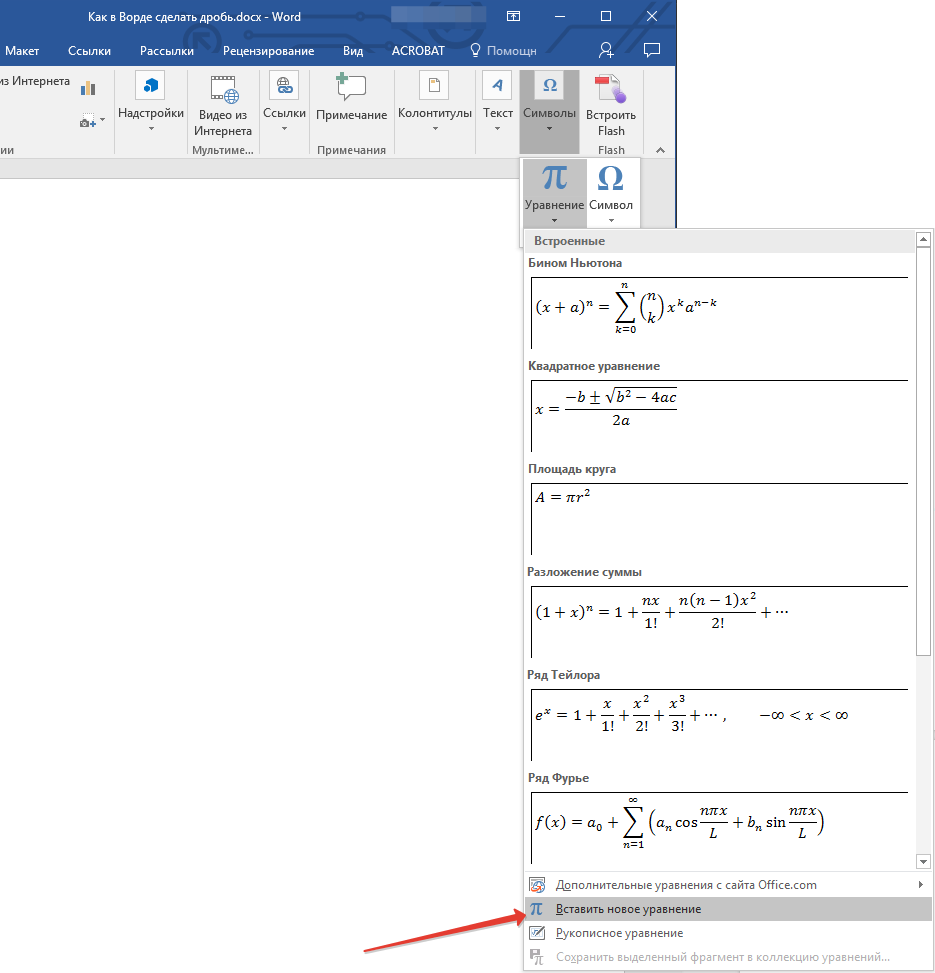
1. Во вкладке “Конструктор”, которая появится на панели управления, нажмите на кнопку “Дробь”.

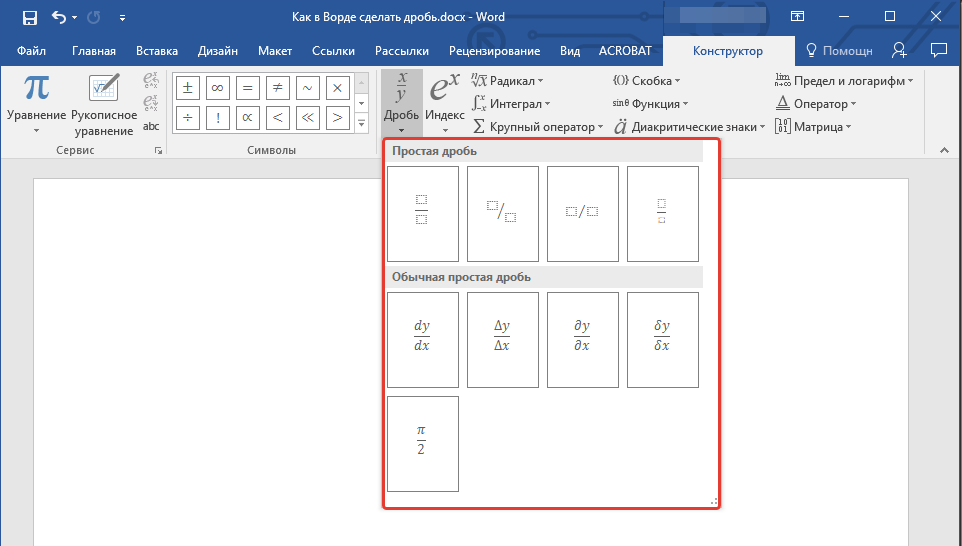
1. В развернувшемся меню выберите в разделе “Простая дробь” тип дроби, которую Вы хотите добавить — через слеш или горизонтальную линию.

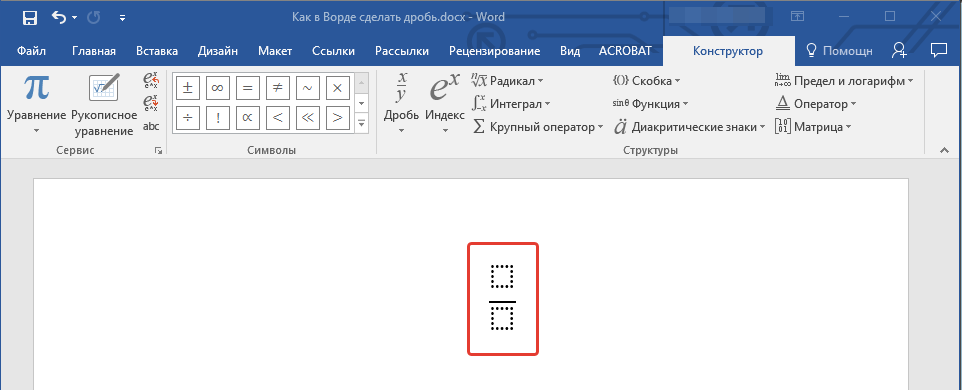
1. Макет уравнения изменит свой внешний вид, впишите в пустые графы необходимые числовые значения.
2. Кликните по пустой области на листе, чтобы выйти из режима работы с уравнением/формулой.

Именно написание дроби через меню вставки нового уравнения является оптимальным решением нашей сегодняшней задачи, тем более, что таким образом можно добавлять выражения обоих типов — и те, что разделены слешем (косой чертой), и те, которые разделяются горизонтальной полосой. Особенно актуально использование этого метода в случае, когда одними дробями работа не ограничивается и требуется писать и другие математические выражения.

Способ 2: Коды полей с ключами

Более простой в своей реализации альтернативой предыдущему решению является написание дробей с горизонтальным разделителем путем ввода и преобразования специального кода поля с ключом. Делается это следующим образом:

1. Установите указатель курсора в том месте текстового документа, где будет записана дробь.

Нажмите на клавиши «Ctrl+F9» (обратите внимание, что на ряде ноутбуков, где F-клавиши по умолчанию выполняют мультимедийные функции, дополнительно может потребоваться нажать клавишу «Fn», то есть сочетание в таком случае будет «Ctrl+Fn+F9»)

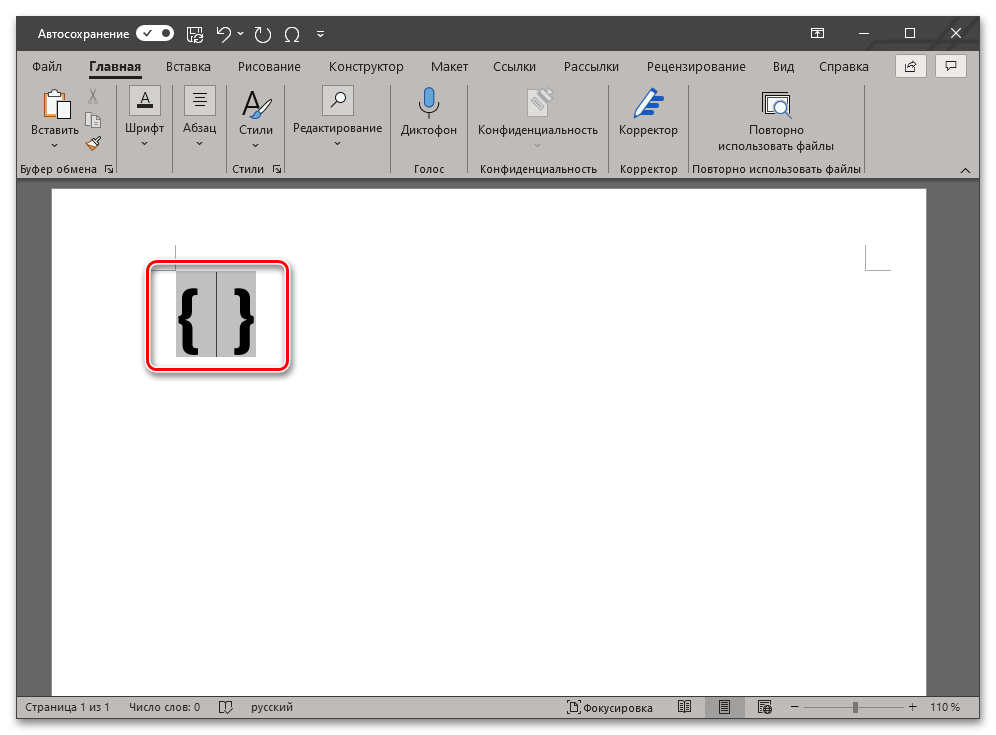
В выбранном месте документа появятся фигурные скобки с мигающей между ними кареткой (указатель курсора). Не перемещаясь из этой области, введите код следующего вида:

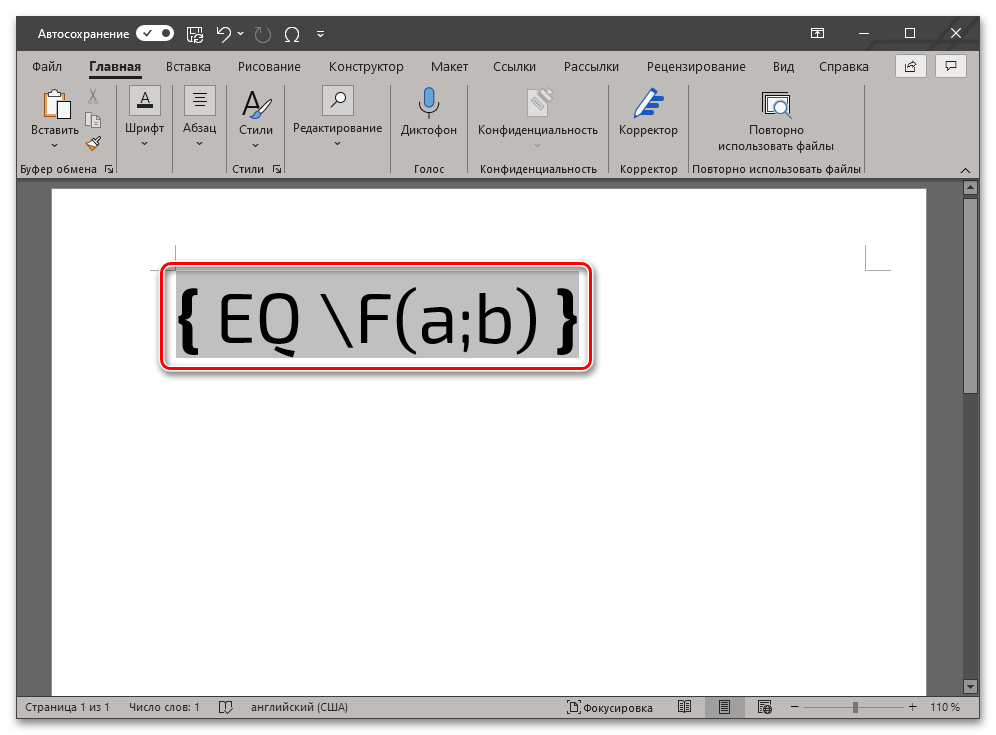
• EQ создает поле для ввода формулы;
• F создает дробь с горизонтальным разделителем и выравнивает относительно этой линии числитель и знаменатель;
• a и b – числитель и знаменатель, то есть вместо этих букв нужно вводить соответствующие им значения. Например, чтобы записать таким образом 2/3, следует использовать указанный ниже код:

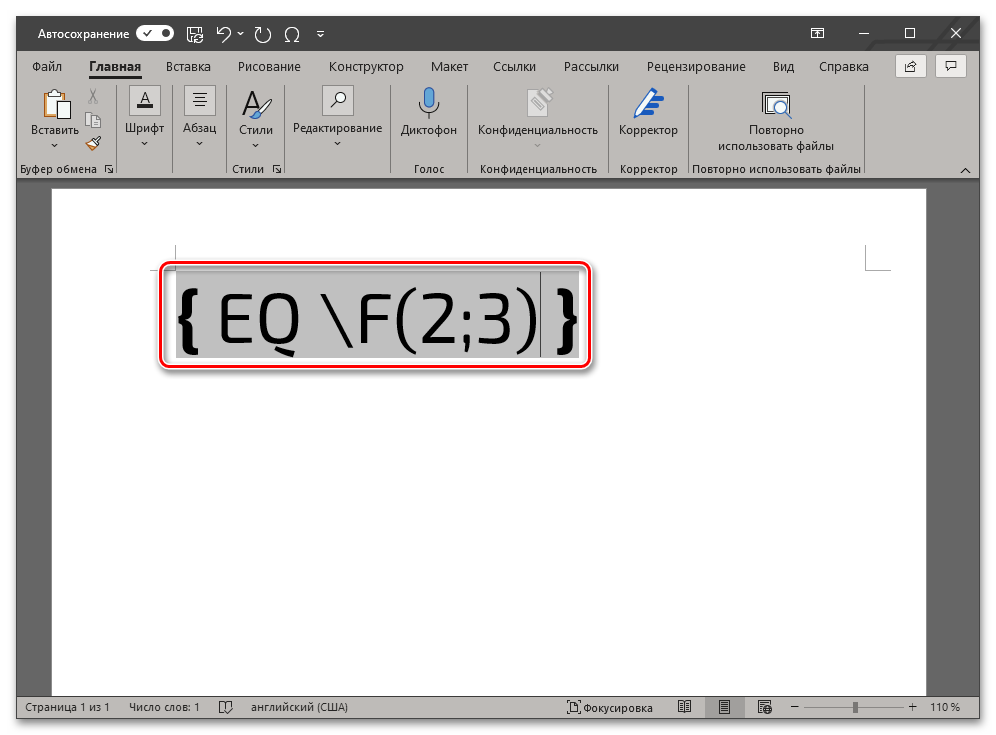
1. Разобравшись со всеми параметрами кода и указав его в том виде, который соответствует желаемой дроби, не перемещая указатель курсора и не покидая обозначенное фигурными скобками поле для ввода, нажмите на клавишу «F9» (опять же, на ноутбуках может потребоваться нажать «Fn+F9»).

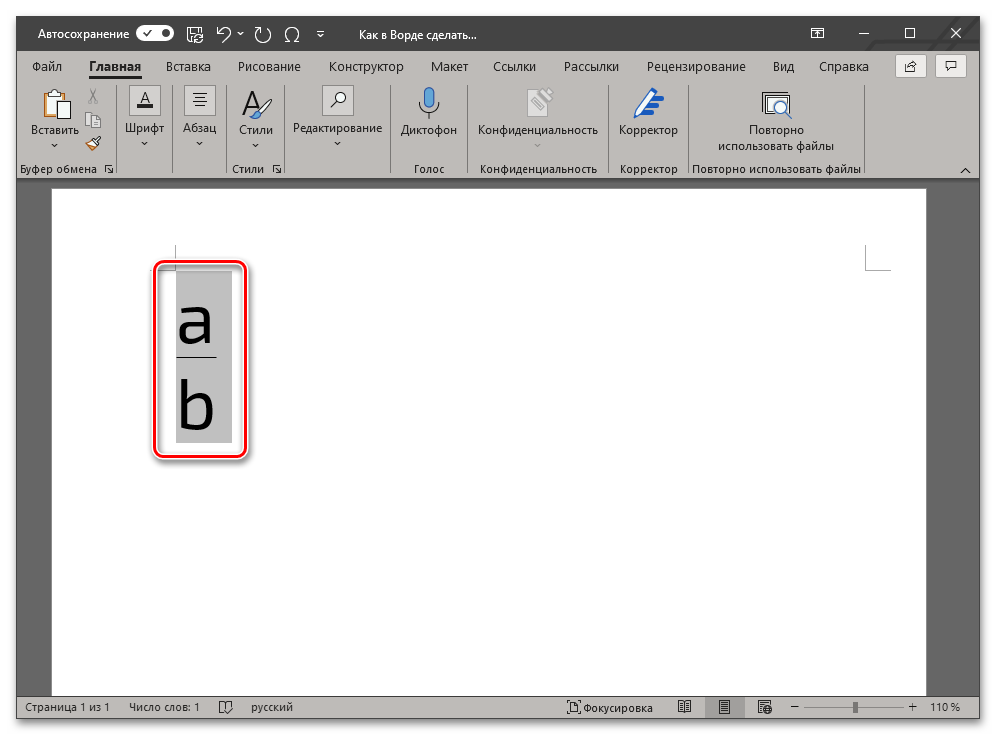
1. В результате выполнения предыдущего шага инструкции код будет преобразован в дробь с горизонтальным разделителем между числителем и знаменателем, что показано на представленных выше и ниже изображениях.

Этот метод является не только более простым и удобным в своем реализации, чем предыдущий, но и лишен характерных для него ограничений. Так, у записанной дроби отсутствует видимое поле (рамка), она выглядит более эстетично и является пригодной для общего форматирования, представляется в виде используемого по умолчанию для ввода текста шрифте, который по необходимости можно изменить на любой другой.

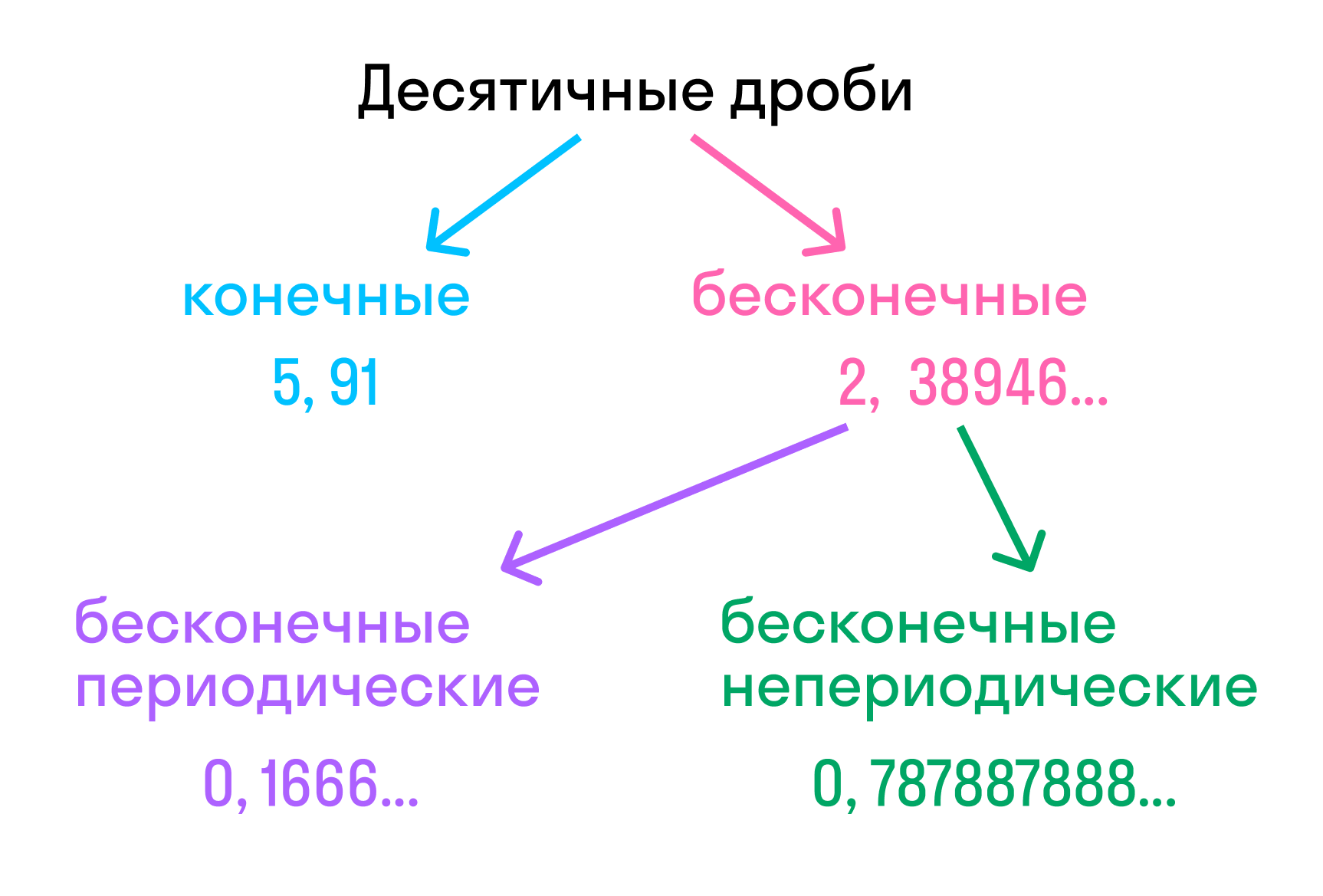
Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.

Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.

В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

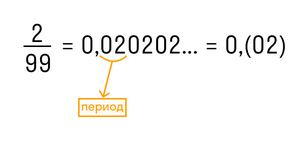
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Виды периодических дробей: чистые и смешанные.

Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).

Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.

Рассмотрим примеры дробей, чтобы научиться определять части и период.

1/3 = 0,3333… = 0,(3)

Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Читаем так: ноль целых три в периоде.

7/12 = 0,583333… = 0,58(3)

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.

17/11 = 1,545454… = 1,(54)

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Читаем так: одна целая пятьдесят четыре сотых в периоде.

25/39 = 0,641025 641025… = 0,(641025)

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.

Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.

пятьдесят четыре сотых в периоде.

9200/3 = 3066,666… = 3066,(6)

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.

Смешанные числа: определения, примеры

Смешанное число — это число, состоящее из натурального числа и обыкновенной дроби. Пишут в виде n

Где n — целая часть, — дробная часть.

Смешанное число равно сумме своей целой и дробной части. То есть

Примеры смешанных чисел

Каждое такое смешанное число содержит целую и дробную части.

Чтобы точно определять, какая именно перед вами дробь, запомните:

• Дробь виданазывается правильной дробью. В ней числитель всегда меньше знаменателя.
• Дробь виданазывается неправильной. В таких дробях числитель больше знаменателя или равен ему.
• Дробь виданазывается смешанной дробью/смешанным числом. Такая дробь состоит из целой части (натуральное число) и дробной части.

Смешанные числа можно складывать, вычитать, умножать и делить. Давайте узнаем, как именно это делать.

1.5.1. Выбор типа дроби и картечи

1.5.1. Выбор типа дроби и картечи

Свинцовая дробь в зависимости от содержания в ней сурьмы и соединений мышьяка производится следующих типов: охотничья твердая (ОТ); охотничья мягкая (ОМ); спортивная твердая (СТ). По способу изготовления дробь может быть штампованной (Ш), литой (Л), катанной (К). В зависимости от норм отклонений диаметров при изготовлении и норм твердости дробь разделяется на первую и высшую категории качества.

В настоящее время охотничья мягкая дробь (ОМ) и картечь (КО) производятся из почти чистого свинца и имеют твердость 5–6 кг/мм?. Твердая дробь должна быть тверже более чем в два раза — до 13–16 кг/мм?.

Мягкая дробь из чистого свинца значительно деформируется при выстреле; периферийные дробины, двигаясь по снарядному входу патронника и каналу ствола, значительно истираются, теряя форму и примерно половину массы, что ухудшает выстрел.

В послевоенные годы, для уменьшения свинцевания канала ствола и предупреждения отравления дичи свинцом, твердую дробь стали покрывать гальваническим способом тонким слоем меди, никеля или хрома. Такая дробь (ее иногда именуют плакированной) меньше деформируется при движении по каналу ствола, что позволяет увеличить ее начальную скорость.

В разное время и в разных странах неоднократно предпринимались попытки изготовить дробь не из свинца, а из других металлов (железа, чугуна), но все они оканчивались неудачей, так как бой ружья дробью из заменителей был хуже по сравнению с боем обычной свинцовой дробью. В СШАдовольно широко применяют стальную дробь; при этом процент раненых, но не взятых птиц резко возрастает.

Правильная шарообразная форма, одинаковый диаметр и вес дроби обеспечивают снаряду при выстреле компактный полет и меньшую растянутость, что и определяет качество выстрела. В связи с этим следует отметить, что размер и качество дроби, поступающей в продажу, в значительной степени не соответствует требованиям, согласно которым обычная литая дробь должна быть круглой с допуском по диаметру в пределах + 0,12 мм, а спортивная дробь, предназначенная для стендовых соревнований, изготовляется с отклонениями по размеру ± 0.1 мм. В торговой же расфасовке дробь мелкого размера практически всегда имеет некруглую форму и много сдвоенных дробин; более крупная дробь напоминает скорее грушу или чечевицу с раковинами и свищами на поверхности, при этом диаметр отдельных дробин резко отличается друг от друга.

Деформированная дробь при вылете из канала ствола ружья ведет себя в воздухе подобно брошенному плоскому камню: она косо отклоняется от основного направления выстрела и, кроме того, теряет скорость гораздо быстрее, чем круглая дробина. Отклонение от центра на 35 м может достигать 2 м и более. Поэтому при тщательном снаряжении патронов такую дробь, особенно первые и нулевые номера, стрелку приходится предварительно прокатывать для придания ей сферической формы, а для получения дроби одного размера и веса ее откалибровывают, просевая через сито. Наиболее перспективным является метод изготовления дроби точной штамповкой, так как штампованная дробь обладает более правильной формой и меньшей разномерностью, чем литая.

Казалось бы, все ясно, необходимо применять только твердую дробь, чтобы максимально использовать возможности дробового выстрела. Однако приобрести патроны, снаряженные твердой дробью, или саму твердую дробь практически нельзя. Наша промышленность многие десятилетия выпускала и выпускает в основном мягкую дробь и картечь. Это делается потому, что в технологическом отношении выпускать мягкую дробь и картечь проще и производительнее.

Многолетняя стрельба мягкой дробью привела к тому, что из-за неэффективности выстрела многие охотники стали применять дробь на несколько номеров более крупную, чем это необходимо для определенной дичи. При такой дроби в снаряде размещается меньше дробин, в дичь на нормальной дистанции попадают лишь одна-две дробины, и она часто погибает вне пределов досягаемости охотника.

Как показали измерения твердости дроби производства иностранных фирм, эта дробь имеет среднюю твердость 15 кг/мм?. Измерения твердости картечи и «Ремингтон» показали, что она имеет твердость в среднем 9 кг/мм?. Во время испытаний патроны с картечью и «Ремингтон» показали в среднем до 15 % большую кучность и до 25 % большую пробиваемость, чем аналогичные патроны отечественного производства.

Дробь и ее виды

Обыкновенная или простая дробь — это число вида a/b , где a — числитель дроби, b — знаменатель дроби. Суть дроби можно объяснить на примере пирога – например, дробь ¼ означает один кусок пирога из 4-ех.

 Правильная — дробь, у которой числитель меньше знаменателя (например, 1/5, 2/9).

 Неправильная — дробь, у которой числитель больше или равен знаменателю (например, 7/2, 5/5).

 Смешанная — дробь, записанная в виде целого числа и правильной дроби. Она представляет собой сумму этого числа и дроби. Любую неправильную дробь можно перевести в смешанную путем выделения целой части (например, 9/4 = 2 ¼).

 Десятичная — дробь со знаменателем 10, 100, 1000 и т.д. (например, 7/10 или 0,7; 9/100 или 0,09). Десятичная дробь записывается в виде целой и дробной части, которые отделяются запятой.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.

Квадрат суммы	(a+b)2 = a2 + 2ab + b2
Квадрат разности	(a-b)2 = a2 — 2ab — b2
Разность квадратов	a2 – b2 = (a – b)(a+b)
Куб суммы	(a+b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности	(a-b)3 = a3 — 3a2b + 3ab2 — b3
Сумма кубов	a3 + b3 = (a + b)(a2- ab+b2)
Разность кубов	a3 — b3 = (a — b)(a2+ ab+b2)

Примеры сокращения дробей с помощью формул сокращенного умножения:

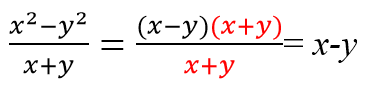
Применяем формулу квадрата разности (a-b)2 = a2 — 2ab — b2 и сокращаем одинаковые многочлены.

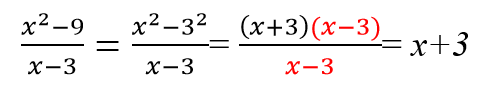
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.

Примеры сокращения дробей за 7 и 8 классы

Сократите дроби:

Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.

• Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
• Поделите числитель и знаменатель на общий множитель.
• Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
• Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
• Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
• Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
• Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.

Возможно тебе будет полезно — Формулы сокращённого умножения (ФСУ)

Арифметические действия с обыкновенными дробями

Сложение и вычитание дробей

При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.

При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем  сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

 Умножение дробей

1. Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
2. При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

 Деление дробей

Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.

Несократимые и сократимые дроби

Если наибольший общий делитель числителя и знаменателя дроби равен единице, то дробь называется несократимой. Например: .

суть несократимые дроби.

Если же наибольший общий делитель числителя и знаменателя отличен от единицы, то дробь называется сократимой. Например:

суть сократимые дроби.

Если числитель или знаменатель дроби отдельно или одновременно являются многочленами, то для решения вопроса о сократимости или несократимости этой дроби необходимо эти многочлены предварительно разложить на целые неприводимые множители, если это возможно. Например, дробь сократима, так как после разложения числителя и знаменателя на множители она принимает вид

Если числитель и знаменатель дроби разделить на их наибольший общий делитель, то получится . несократимая дробь, тождественно равная данной дроби.

Примеры сокращения дробей:

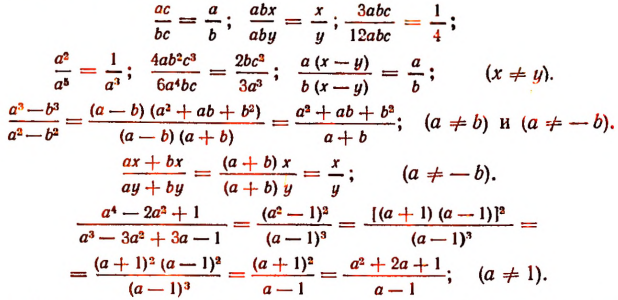
Сократить дробь — это значит разделить числитель и знаменатель этой дроби на какой-нибудь их общий множитель.

Полученная после этого новая дробь будет тождественно равна первоначальной дроби. Например,

(Здесь дробь сокращена только на общий множитель b.)

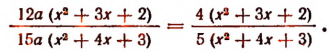
(Здесь дробь сокращена только на За.)

Примечание:

Выражение по форме дробное, но по существу целое, так как оно тождественно равно выражению 5аb. Однако между выражениями и 5ab имеется еще и другое различие, а именно выражение при а = 0 смысла не имеет, тогда как выражение 5ab при а = 0 имеет смысл, так как принимает определенное значение нуль.

Перевод периодической дроби в обыкновенную

Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.

Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.

Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:

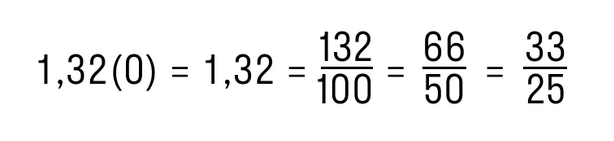
Вот и ответ!

Рассмотрим пример, в котором период дроби отличен от нуля.

Как записать периодическую дробь 10,0219(37) в виде обыкновенной:

1. Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k.

   В нашем примере k = 2.

2. Считаем количество цифр, которые стоят после запятой, но до периода десятичной дроби. Обозначаем количество цифр буквой m.

   m = 4.

3. Запишем все цифры после запятой: в том числе и цифры из периода в виде натурального числа.

   Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.

   a = 021937 = 21 937

4. Теперь запишем все цифры, которые стоят после запятой, но до периода, в виде натурального числа. Если вначале до первой значащей цифры идут нули, то отбрасываем их. Обозначим полученное число — b.

   b = 0219 = 219

5. Подставляем найденные значения в формулу, где Y — целая часть бесконечной периодической дроби.

   Y = 10

Теперь осталось подставить все найденные значения в формулу и получить ответ:

Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.

Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:

0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + ..

Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q).

Пример. Перевести периодическую дробь 0,(7) в обыкновенную.

Как решаем:

1. Запишем 0,(7) = 0,7 + 0,07 + 0,007 + ..

   Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1.

2. Применим формулу b/(1-q):

   0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 — 0,1) = 0,7/0,9 = 7/9.

Ответ: 7/9.

Итак, есть два вида периодических дробей. Сейчас расскажем, чем отличаются способы их преобразования в обыкновенные дроби.

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

Правильная и неправильная дробь

Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Определение дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

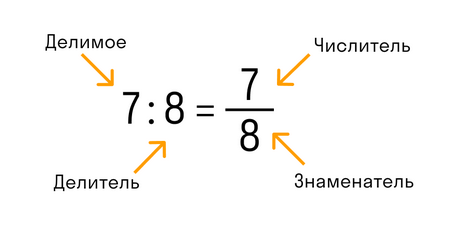
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,7
• 6,51
• 9,932

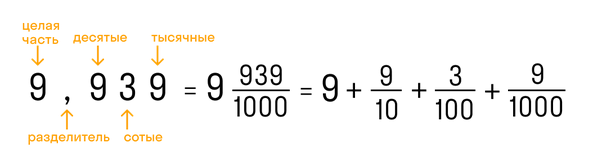
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Материал

Самый распространенный вариант материала для дроби – свинец. Именно он обладает самыми лучшими свойствами:

• легкоплавкость;
• дешевизна;
• тяжесть.

Из свинца достаточно просто изготовить дробь в домашних условиях. Однако многие страны мира отказались от его использования, так как он токсичный и несет угрозу окружающей среде.

Каленый свинец – это та же дробь из свинца, но с примесями других химических веществ: мышьяк, олово или сурьма.

Сталь – еще один распространенный материал, который к тому же не деформируется. Однако у него больше минусов, чем плюсов. Сталь быстро утрачивает нужную скорость и способствует быстрому износу ствола оружия.

Какая дробь бывает еще? На сегодняшний день самой дорогой и лучшей по всем характеристикам считается плакированная дробь. Это все тот же свинец, но покрытый мельхиором или никелем.

Действия с правильными дробями, как найти

Правильные дроби можно встретить при решении множества задач по математике. Для них предусмотрены все действия, которые выполняют с обыкновенными дробями.

Приведение к общему знаменателю

Перед тем, как сравнить, сложить или вычесть дроби, требуется выполнить их преобразование. В результате арифметических действий дроби должны пробрести одинаковые знаменатели. К примеру, имеется пара дробей:

ab

cd

Последовательность операций:

1. Найти минимальное единое кратное для знаменателей: M=b,d.
2. Умножить числитель и знаменатель первой дроби на Mb.
3. Умножить числитель и знаменатель второй дроби на Md.

В результате знаменатели первой и второй дроби становятся одинаковыми и равными M. Допустимо заменить минимальное единое кратное при решении несложных примеров на какое-либо другое общее кратное. К примеру, таким кратным может стать произведение знаменателей.

Сравнение

С целью сравнения пары обыкновенных дробей необходимо выполнить операцию приведения их к единому знаменателю. Далее следует сравнить числители дробей, которые в итоге получились. Если числитель больше, то и дробь считается больше.

Сложение и вычитание

Прибавить одну обыкновенную дробь к другой обыкновенной дроби можно. Но перед этим требуется выполнить приведение этих дробей к единому знаменателю. После такой операции находят сумму числителей, а знаменатели оставляют без изменений.

При умножении двух обыкновенных дробей требуется выполнить умножение их числителей и знаменателей:

ab·cd=acbd

Возведение в степень и извлечение корня

Дроби можно возводить в степень. При этом необходимо выполнить арифметическое действие возведения в степень отдельно со знаменателем и числителем этой дроби:

abn=anbn,b≠.

Перевод других видов дробей в правильную форму

Для того чтобы перевести неправильную дробь в правильную, либо для выполнения обратного действия, требуется соблюдать определенный порядок. Прямой перевод невозможен. Результатом подобной операции будет являться преобразованная запись, которая содержит в себе целую, а также дробную части. Последовательность действий:

• упростить запись дробного отношения;
• вычислить произведение целой части и делителя дробной части;
• сложить результата умножения с числителем;
• полученную сумму записать в качестве делимого преобразованного выражения;
• знаменатель нужно оставить прежним.

С помощью достаточно простого метода удобно переводить числа из одной формы в какую-либо другую. Данный алгоритм можно записать в виде математического уравнения:

na÷b=((n×b)+a)÷b

Смешанное отношение представляет собой сумму из целого и части. Для того чтобы понять, как преобразовать дроби, следует выполнить сложение в качестве арифметического действия.  В процессе первое слагаемое нужно записать в виде неправильной дроби путем деления целого на 1. Далее целесообразно воспользоваться правилом сложения дробей. Выполняется поиск общего знаменателя, дополнительных множителей, сложение в числителе. Формула имеет такой вид:

na÷b=n÷1+a÷b=((n×b)+a)÷b

Неправильную дробь превратить в обычную можно с помощью перевода ее в смешанную. В процессе выражение записывают в виде суммы натурального числа и правильной дроби:

1. Найти отношение делимого к делителю.
2. Полученный результат записать в числителе.
3. Знаменатель будет равен исходному числу, стоящему в делителе.
4. Приписать частное к выражению в виде целой доли.

Более простой способ преобразования дробей заключается в представлении делимого, как суммы дробей

При этом важно, чтобы при делении одной из них не было остатка:. m÷n=(k+c)÷n=k÷n+c÷n

m÷n=(k+c)÷n=k÷n+c÷n

Здесь целое число k÷n, а c÷n является правильной дробью.

Правильные и неправильные дроби, определения, примеры

В основе разделения дробей на правильные и неправильные лежит сравнение числителя и знаменателя в пределах одной дроби.

Определение 7

Правильная дробь – это обыкновенная дробь, в которой числитель меньше, чем знаменатель. Т.е., если выполняется неравенство m < n, то обыкновенная дробь mn является правильной.

Неправильная дробь — это обыкновенная дробь, числитель которой больше или равен знаменателю. Т.е., если выполняется неравенство undefined, то обыкновенная дробь mn является неправильной.

Приведем примеры: — правильные дроби:

Пример 1

59, 367, 138514;

— неправильные дроби:

Пример 2

1313, 573, 901112, 167.

Также возможно дать определение правильных и неправильных дробей, опираясь на сравнение дроби с единицей.

Определение 8

Правильная дробь – обыкновенная дробь, которая меньше единицы.

Неправильная дробь – обыкновенная дробь, равная или бОльшая единицы.

Например, дробь 812 – правильная, т.к. 8 12< 1. Дроби 532 и 1414 являются неправильными, т.к. 532 > 1, а 1414 = 1.

Немного углубимся в размышление, почему дроби, в которых числитель больше или равен знаменателю получили название «неправильных».

Рассмотрим неправильную дробь 88: она сообщает нам, что взято 8 долей предмета, состоящего из 8 долей. Таким образом, из имеющихся восьми долей мы можем составить целый предмет, т.е. заданная дробь 88 по сути представляет целый предмет: 88=1. Дроби, в которых числитель и знаменатель равны, полноценно заменяет натуральное число 1.

Рассмотрим также дроби, в которых числитель превосходит знаменатель: 115 и 363. Понятно, что дробь 115 сообщает о том, что из нее мы можем составить два целых предмета и еще останется одна пятая доля. Т.е. дробь 115 – это 2 предмета и еще 15 от него. В свою очередь, 363 – дробь, означающая по сути 12 целых предметов.

Указанные примеры дают возможность сделать вывод, что неправильные дроби возможно заменить натуральными числами (если числитель без остатка делится на знаменатель: 88 = 1; 363 = 12) или суммой натурального числа и правильной дроби (если числитель не делится на знаменатель без остатка: 115 = 2 + 15). Вероятно, потому такие дроби и получили название «неправильных».

Здесь также мы сталкиваемся с одним из важнейших навыков работы с числами.

Определение 9

Выделение целой части из неправильной дроби – это запись неправильной дроби в виде суммы натурального числа и правильной дроби.

Также отметим, что существует тесная взаимосвязь между неправильными дробями и смешанными числами.

Умножение смешанных чисел

Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа

Умножение смешанного числа на смешанное число

Первое правило умножения смешанных чисел Чтобы умножить одно смешанное число на другое, нужно перевести обы смешанных числа в неправильные дроби, а затем выполнить умножение по правилу умножения дробей

Пример. Выполните умножение смешанного числа и

Как решаем:

Запишем выражение

Следуя правилу, переведем смешанные числа в неправильные дроби.

Выполним умножение:

Из полученной неправильной дроби выделяем целую часть

Ответ:

Умножение смешанного числа на обыкновенную дробь

Второе правило умножения смешанных чисел Чтобы выполнить умножение смешанного числа и обыкновенной дроби, представьте смешанное число в виде неправильной дроби и выполните умножение дробей.

Пример. Умножьте смешанное число на обыкновенную дробь

Как решаем:

Запишем выражение

Представим смешанное число в виде неправильной дроби.

Выполним умножение дробей

Выделим из полученной неправильной дроби целую часть

Ответ:

Умножение целого числа на дробь

Третье правило умножения смешанных чисел Чтобы умножить целое число на дробь, просто умножьте это число на числитель дроби.

Пример. Выполните умножение числа 7 на обыкновенную дробь

Как решаем:

Запишем выражение:

Выделим из получившейся неправильной дроби целую часть

Ответ: